Corruption is notoriously widespread in data collection, and has been widely studied through the introduction of various corruption models addressing specific cases. Motivated by the existence of a zoo of models, not yet well-related or compared to each other, we worked on a framework for unifying and studying corruption in the following paper:
Corruptions of Supervised Learning Problems: Typology and Mitigations
We started by considering Markovian corruptions, i.e., a Markov kernel acting on a data-generating probability distribution. However, we also gave a general notion of corruption, including non-Markovian distribution changes as well as loss or model class. Our Markovian corruption subsumes many models of corruption — others are not! Famous examples are Mutually Contaminated Distributions and Selection Bias. This further underlines the need for a Theory of General Corruption.
Secondly, we studied how corruption affects learning problems. Since learning for us means risk minimization, we proved Bayesian Risk equalities (in the sense of the DPE paper) that allowed us to define a notion of “equivalent corrupted problems”. Interestingly, a Markovian corrupted problem is equivalent in Bayes Risk to a problem with jointly corrupted loss and model class.
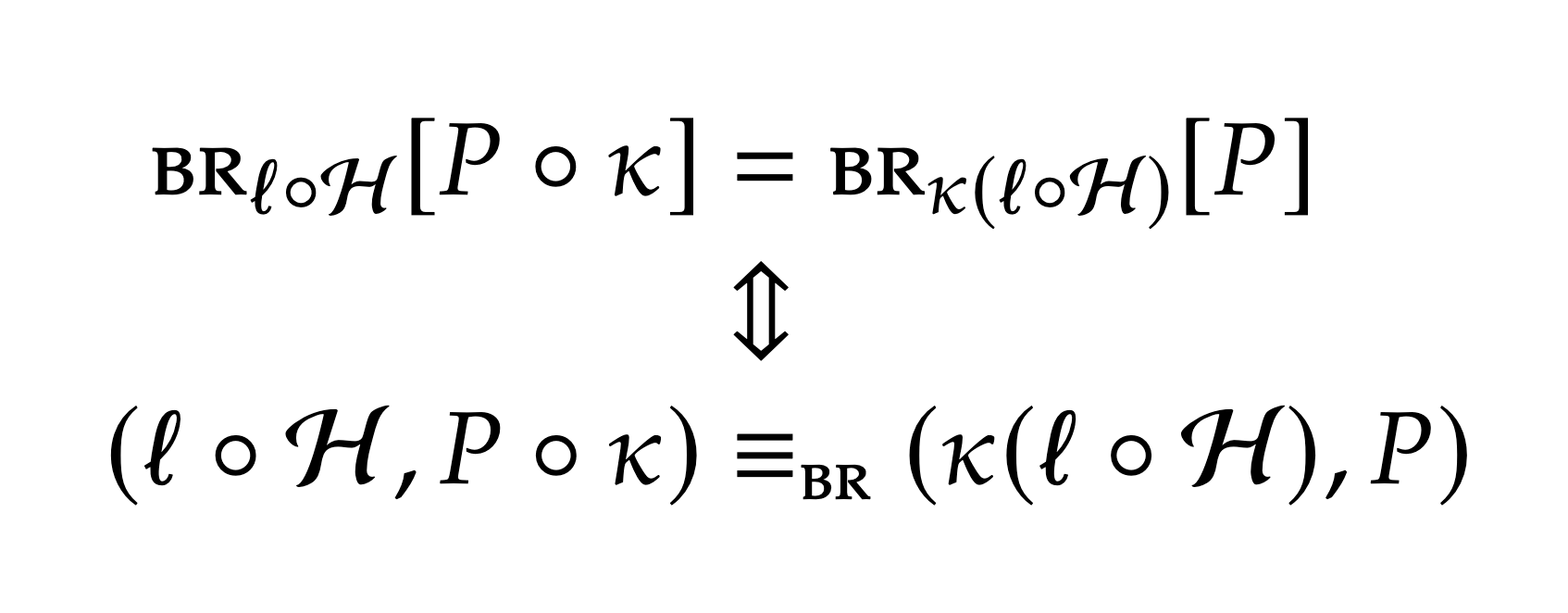
This has consequences in terms of possible corruption mitigations, since as we showed, loss correction techniques get harder to design and formulate in the case of general corruption that is not only label noise.