Machine learning research is notoriously fast paced. Can one get off the treadmill and embrace a notion of slow science? I am pleased to be able to argue yes by example! Recently I have had two works published with a very long gestation.
The first Geometry and Calculus of Losses reports work that started in 2012 (not a typo). It presents a beautiful (yes it is!) geometric theory of loss functions, with all sorts of interesting connections to convex geometry and economics. 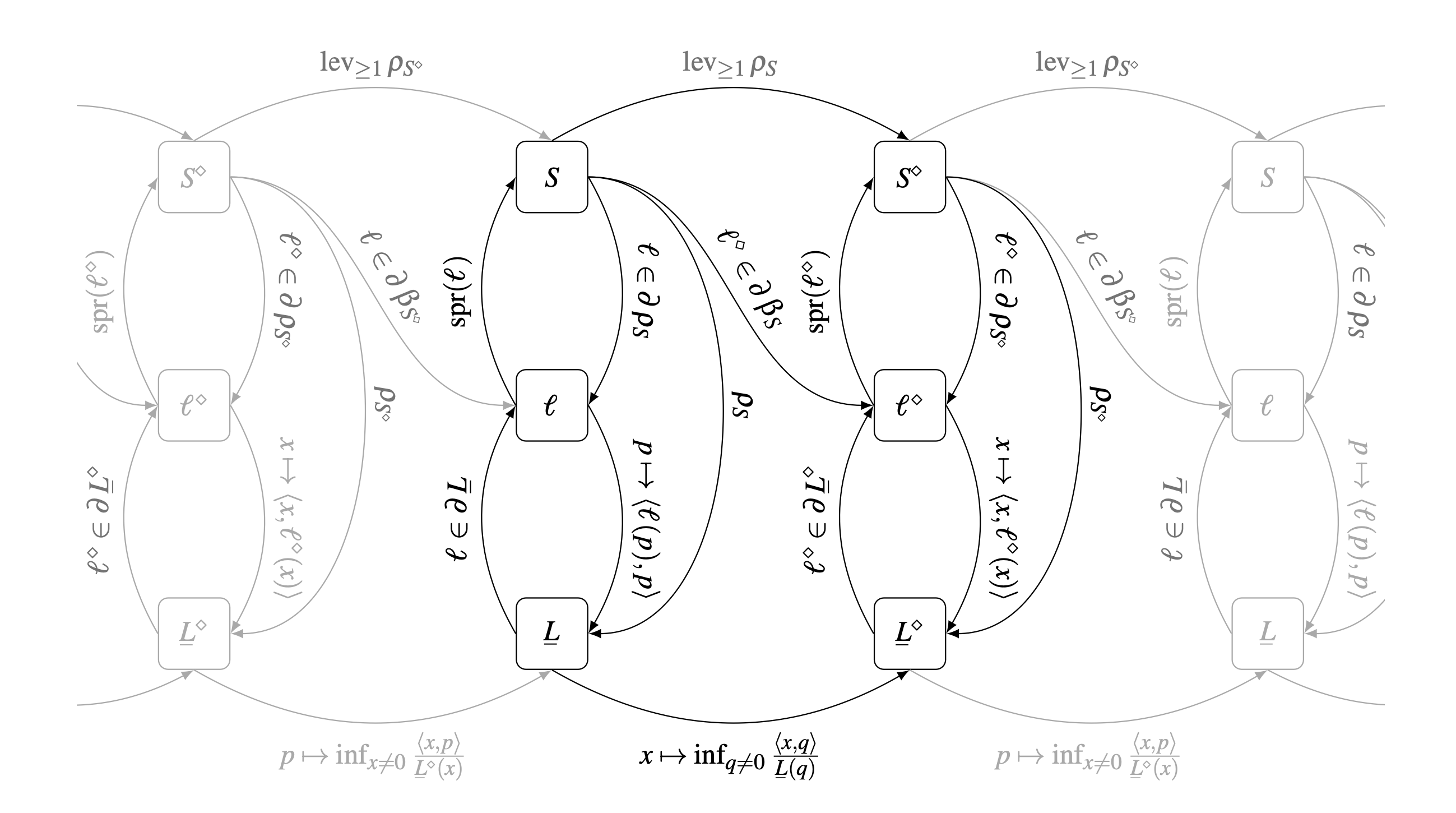
The second Information Processing Equalities and the Information-Risk Bridge builds upon the first and revisits what is arguably the most basic result in information theory, namely the "information processing inequality." It shows that in fact it can be written as an equality, albeit one with different measures of information on each side. It also presents a more general theory of the bridge between information and risk, showing these are generally two sides of the same coin. The earliest version of one of the main results was worked out in 2007 (again not a typo). It was published last week ... after some 17 years!
This work took a very long time largely because of external events (my work on Technology and Australia's Future which totally absorbed my efforts for 2.5 years), the absorption of NICTA into CSIRO (another several years, not at all pleasant), my move from Australia to Germany, and a serious health issue in 2022 (also no fun).
I am pleased to see both these works finally published. :-)
Bob